目录

• 约定

• Lambert Lighting

• Half-Lambert Lighting

• Phong

• Blin-Phong Lighting

• Wrap Lighting

• Gouraud Lighting

• Banded Lighting

• Minnaert Lighting

• Oren-Nayar Lighting

• BackLight or CheapSSS 背光|简易次表面散射

• Anisotropic Lighting

• PBR

• PBR Anistropy基于物理的各项异性高光

• ClearCoat清漆

• Cloth布料

约定

L 光照方向

N 法线方向

V 视角方向

T 切线方向

H 半角向量

这些向量 为世界空间下的向量 且是 单位向量

Lambert Lighting

兰伯特反射(Lambert)是最常见的一种漫反射，它与视角无关，即从不同的方向观察并不会改变渲染结果。

//Lambert
FinalColor=saturate(dot(N,L))

Half-Lambert Lighting

Half-Lamber是Valve公司提出来的算法，其为了解决Lambert公式在灰面太暗的问题。这是一个经验公式，没啥依据可言。

 //Half-Lambert
FinalColor = pow(dot(N,L)*0.5+0.5,2);

比原Lambert亮了许多

既然是经验公式，那么我也瞎写一个

 //Half-Lambert-XiaJiBa-Write
FinalColor = dot(N,L)*0.5+0.5;

同样更亮了，

既然我能瞎写，也有大佬在我之前就瞎写了，且起了个名字，叫DiffuseWrap

//_WrapValue 范围为[0.5,1]
FinalColor = pow(dot(N,L)*_WrapValue+(1-_WrapValue),2);

_WrapValue设置成0.8

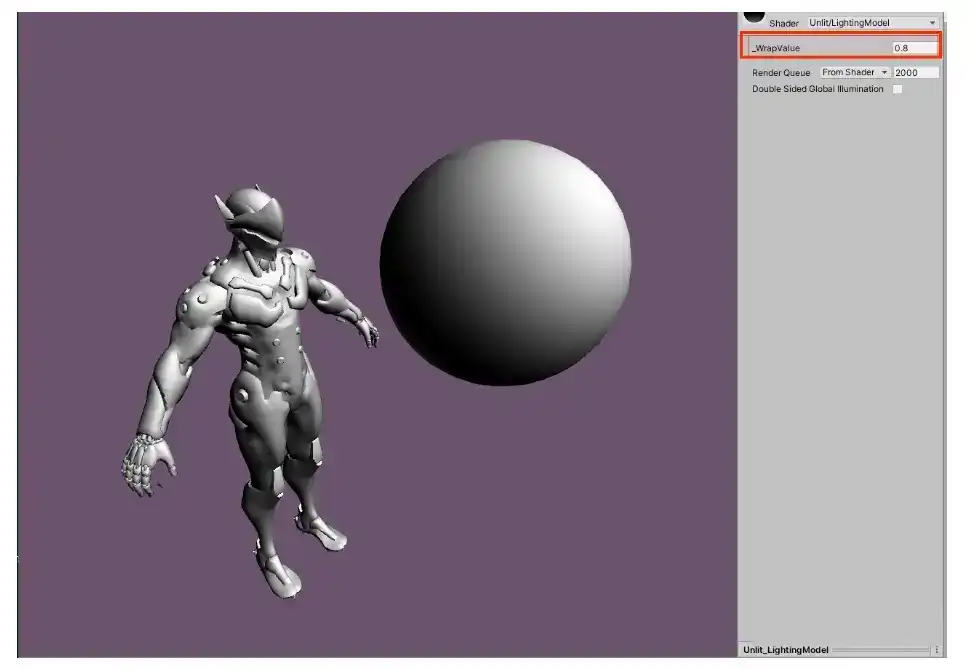
如果不小心将_WrapValue调成了1.4你还能看到光"透射"的效果，没错近似的次表面散射就是用这种方法做的，只不过要把视角计算进去！

同样地可以开脑洞，把代码改成这种调调效果

//_WrapValue 范围为[0.5,1]
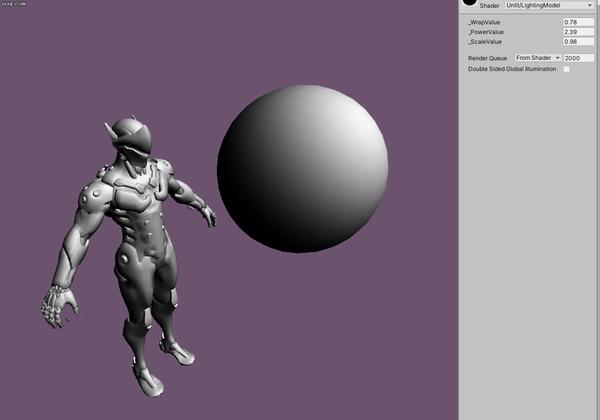
FinalColor = pow(dot(N,L)*_WrapValue+(1-_WrapValue),_PowerValue)*_ScaleValue;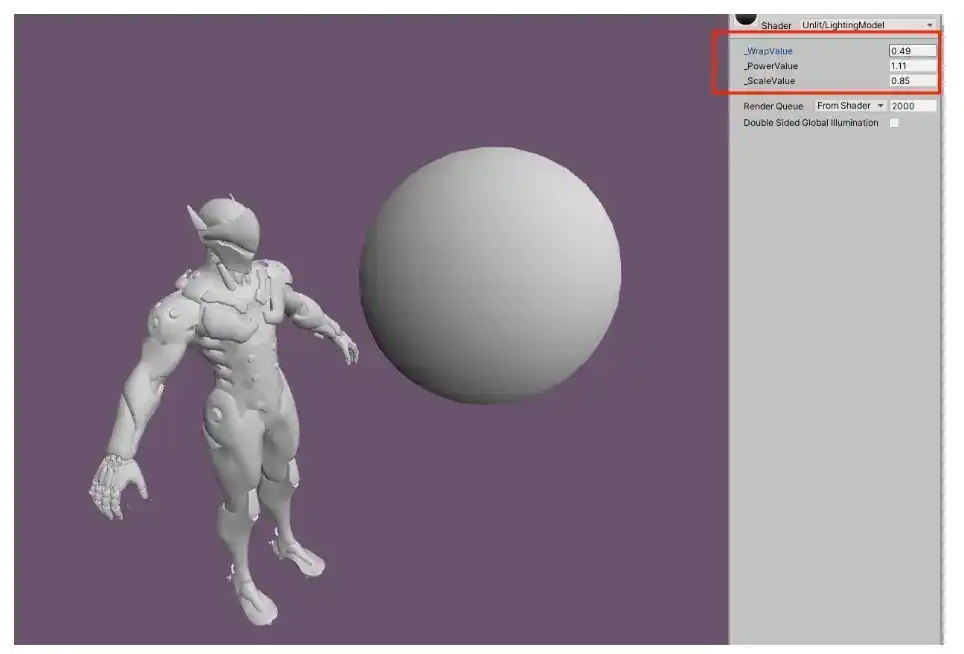

一顿狂调

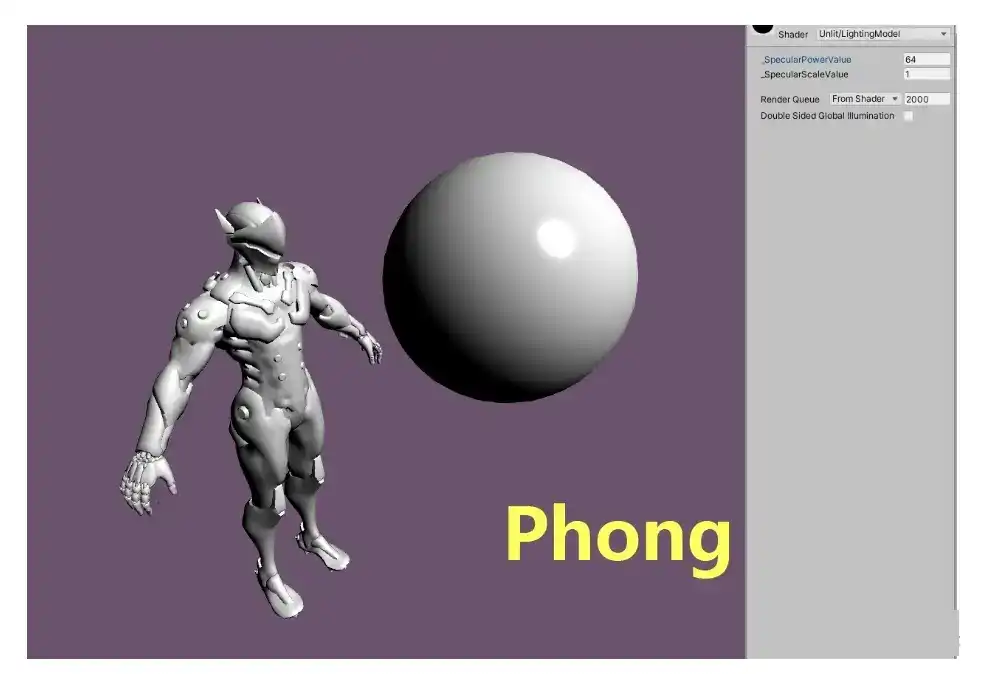
Phong

Phong模型用来模拟高光效果，它认为 从物体表面反射出的光线中包括 粗糙表面的漫反射与光滑表面高光 两部分。

//Phong
float3 R = reflect(-L,N);
// float3 R = normalize(  -L + 2* N* dot(N,L) );
float VR = saturate(dot(V,R));
float NL = saturate(dot(N,L));
float4 Specular = pow(VR,_SpecularPowerValue)*_SpecularScaleValue;
float4 Diffuse = NL;
FinalColor = Specular + Diffuse;

Diffuse

Specular

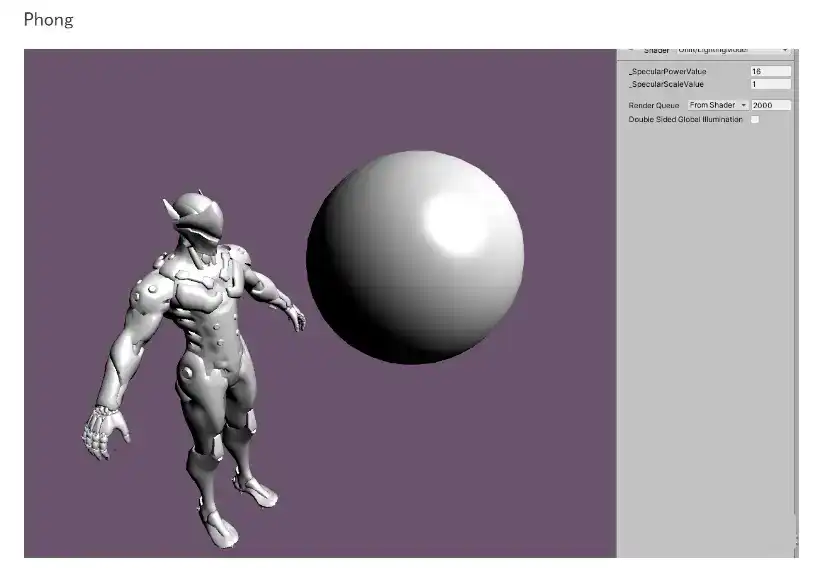
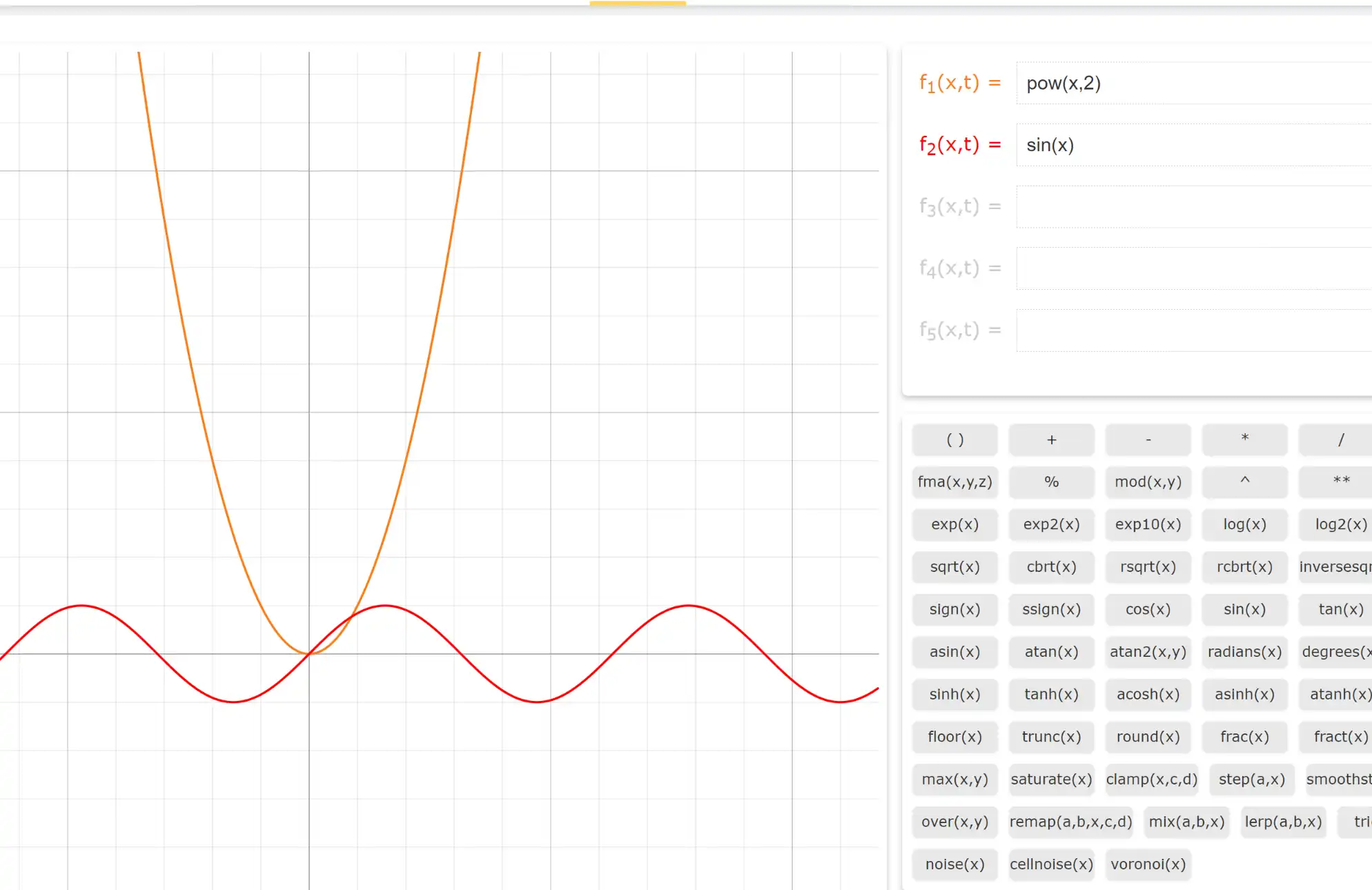
注意Pong公式 pow(VR,_SpecularPowerValue)*_SpecularScaleValue 使用了一个pow函数，其实我刚开始看到的时候也纳闷为什么要用pow函数，后来想通了，其作用就是控制函数曲线调节数值，调节PowerValue 与 PowerScale可以调节曲线数值，和波函数 y=A(Wx+B)+C 中的 AWBC一个作用。

可以在这里作图数学曲线：https://talkartist.cn/discover/tagraph

Blin-Phong Lighting

Jim Blinn在Phong的基础上进行了改进，引入了半角向量，即视角与光线中间的方向。其得到的高光结果比Phong更"光滑"。

//Blin-Phong
float3 H = normalize(V+L);
float NH = saturate(dot(N,H));
float NL = saturate(dot(N,L));
float4 Specular = pow(NH,_SpecularPowerValue)*_SpecularScaleValue;
float4 Diffuse = NL;
FinalColor = Specular + Diffuse;

对比一样，相同参数的效果

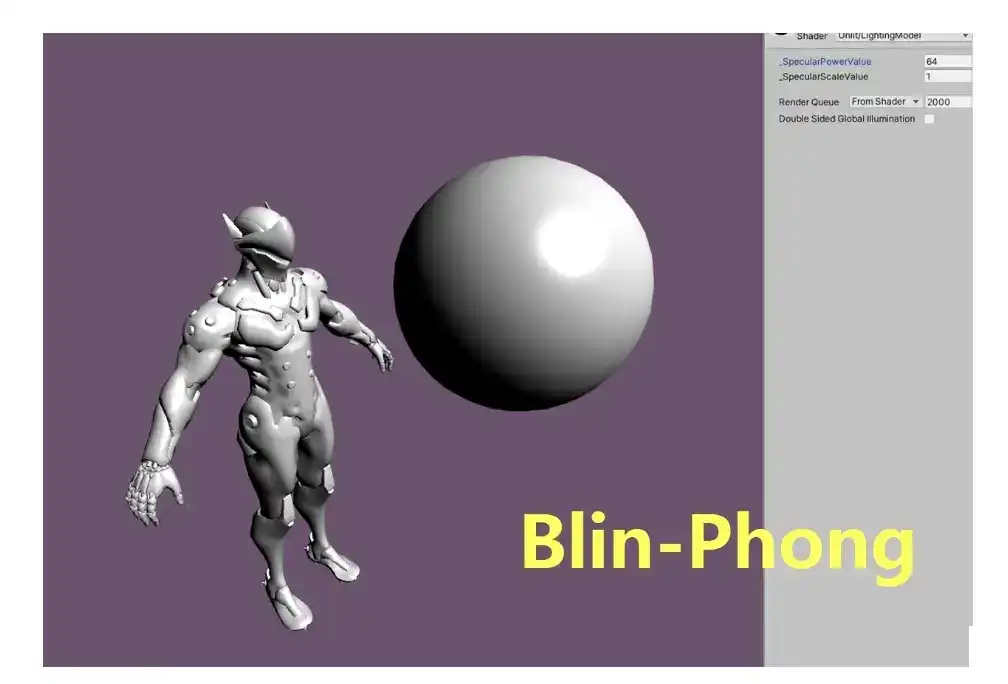
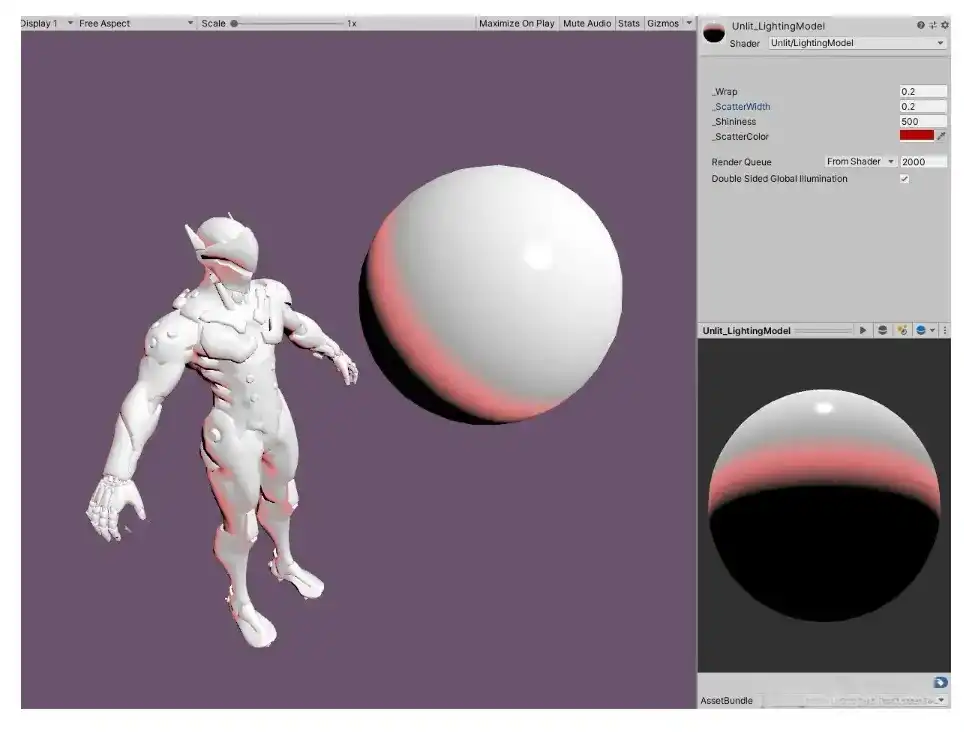
Wrap Lighting

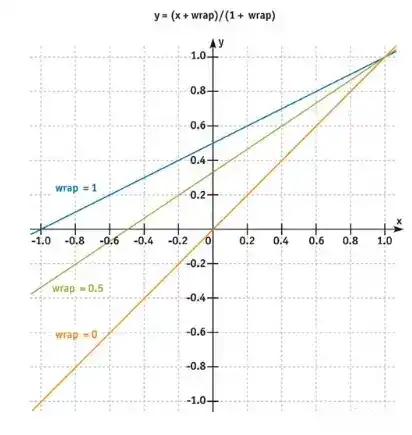
正常情况下，当表面的法线对于光源方向垂直的时候，Lambert漫反射提供的照明度是0。而环绕光照修改漫反射函数，使得光照环绕在物体的周围，越过那些正常时会变黑变暗的点。

float NL = dot(N,L);
float NH = dot(N,H);
float NLWrap = (NL + _Wrap)/(1 + _Wrap);
//add color tint at transition from light to dark
//在从明到暗的转换中添加颜色色调
float scatter = smoothstep(0,_ScatterWidth,NLWrap) * smoothstep(_ScatterWidth*2,_ScatterWidth,NLWrap);
float specular = pow(saturate(NH),_Shininess);
float3 diffuse = max(NLWrap,0) + scatter* _ScatterColor;

FinalColor.rgb = diffuse + specular;

Gouraud Lighting

简单来说Gouraud就是在VertexShader而不是在FragmentShader中计算光照的Phong模型。

在顶点中计算光照后，再在Fragment中插值。

//在顶点中计算光照
v2f vert (appdata v)
{
    v2f o = (v2f)0;//初始化v2f
    o.vertex = UnityObjectToClipPos(v.vertex);
    o.uv = v.uv;
    float3 L = normalize(WorldSpaceLightDir(v.vertex));
    float3 V = normalize(WorldSpaceViewDir( v.vertex));
    float3 N = normalize(UnityObjectToWorldNormal(v.normal));
    float3 R = normalize(reflect(-L,N));

    float Diffuse = saturate(dot(N,L));
    float VR = saturate(dot(V,R));
    
    float Specular = pow(VR,_GouraudPowerValue)*_GouraudPowerScale;
    //仅显示高光
    //o.FinalColor.xyz = 0 + Specular;
    //加上Diffuse
    o.FinalColor.xyz = Diffuse + Specular;

    return o;
}
//在PS中硬件会自动插值
float4 frag (v2f i) : SV_Target
{
    return i.FinalColor;
}

Gouraud 高光

Phong 高光

在顶点中计算光照的可以节省一些性能，但是效果没那么好。

Gouraud 漫反射+高光

Phong 漫反射+高光

Banded Lighting

这个方法更像一个Trick而不是一个光照模型。基本原理就是对NdotL做条状化处理，卡通渲染效果的二分卡边原理与此类似。

//Banded Lighting
float NL = saturate(dot(N,L));
float BandedStep = 6;
float BandedNL = floor(NL*BandedStep)/BandedStep;
float4 Diffuse = BandedNL;
FinalColor = Diffuse;

整点颜色渐变

//Banded Lighting
float NL = (dot(N,L))*0.5+0.5;//[-1,1] => [0,1]
// float _BandedStep = 6;
float BandedNL = floor(NL*_BandedStep)/_BandedStep;
float4 Diffuse = lerp(_ColorA,_ColorB,BandedNL);
// float4 Diffuse = smoothstep(_ColorA,_ColorB,BandedNL);
FinalColor = Diffuse;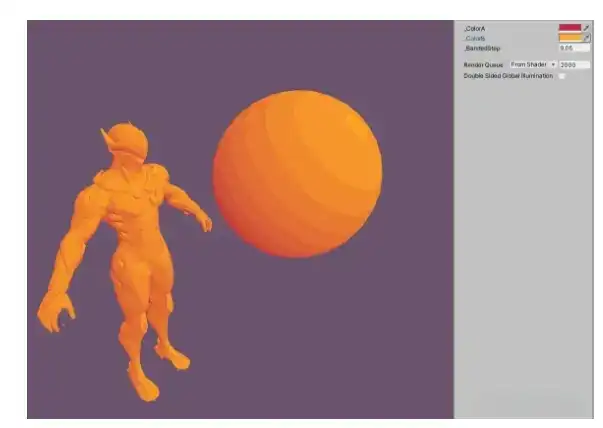

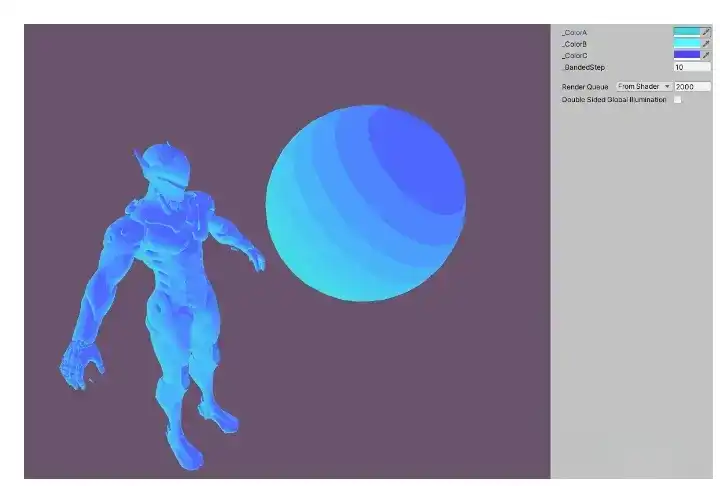
三个颜色渐变

 //Banded Lighting
float NL = (dot(N,L))*0.5+0.5;
// float _BandedStep = 6;
float BandedNL = floor(NL*_BandedStep)/_BandedStep;
float4 C1 = lerp(_ColorA,_ColorB,BandedNL);
float4 C2 = lerp(_ColorB,_ColorC,BandedNL);
float4 Diffuse = lerp(C1,C2,BandedNL);
// float4 Diffuse = smoothstep(_ColorA,_ColorB,BandedNL);
FinalColor = Diffuse;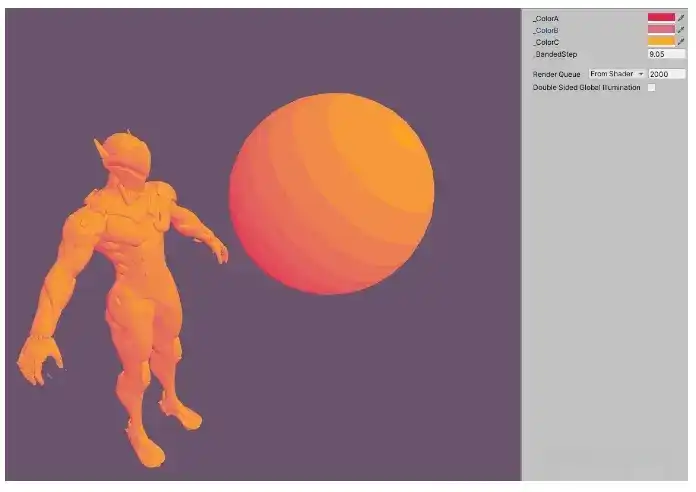

Minnaert Lighting

Minnaert光照主要是用来模拟月球光照的，因为月球上没有空气，所以没有大气散射象限，只有光照到的部分是亮的，其他的部分都是暗的。可以看下图感受一下:

这是月球的白天，阿波罗号

在月球背面的嫦娥号

 //Minnaert Lighting
float NL = saturate(dot(N,L));
float NV = saturate(dot(N,V));
// float _Roughness = 0.5;
float4 Minnaert = saturate(pow(NL*NV,_Roughness)*NV);
FinalColor = Minnaert;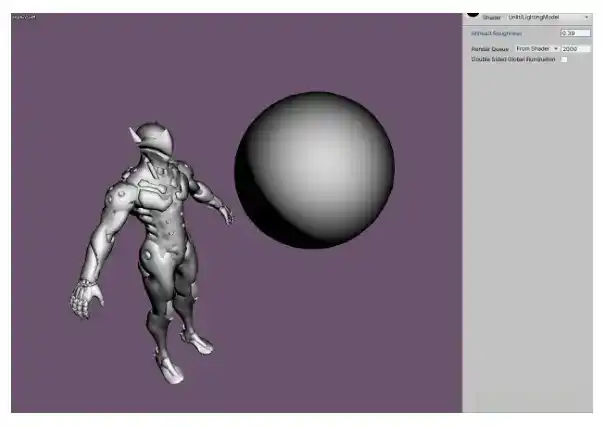

Oren-Nayar Lighting

此模型用来描述光在粗糙表面的反射情况，相比于Lambert模型，它考虑了 粗糙度参数，常用来模拟比较粗糙的表面。比如游戏风之旅人的沙漠就是在Oren-Nayar的模型上做的改进。(https://www.gdcvault.com/play/1017742/Sand-Rendering-in)

原Oren-Nayar模型公式,公式中光线方向与反射方向是用球坐标系表示的，

这是一个转化后便于写代码的版本:

注意arccos 是arc cos，即反余弦函数

参考: Oren–Nayar reflectance model - Wikipedia

float NL = saturate(dot(N,L)); 
float NV = saturate(dot(N,V)); 
float theta2 = _Roughness_Roughness; 
float A = 1 - 0.5(theta2/(theta2 +0.33)); 
float B = 0.45 (theta2/(theta2+0.09)); 
float acosNV = acos(NV); 
float acosNL = acos(NL); 
float alpha = max(acosNV,acosNL); 
float beta = min(acosNV,acosNL); 
float gamma = length(V - NNV) * length(L - N*NL); 
float Diffuse = 1; 
float OrenNayer = Diffuse * NL (A+ Bmax(0,gamma)*sin(alpha)*tan(beta)); 
FinalColor = OrenNayer;

狂调参数

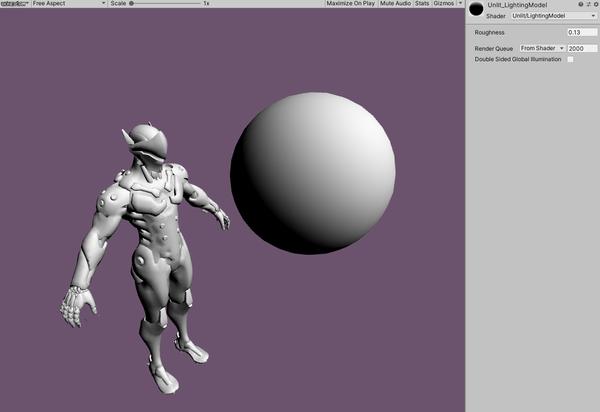
加一张Roughness贴图

//Oren-Nayer float roughness = tex2D(_RoughnessTex,i.uv).r _Roughness; 
float NL = saturate(dot(N,L)); 
float NV = saturate(dot(N,V)); 
float theta2 = roughnessroughness; 
float A = 1 - 0.5*(theta2/(theta2 +0.33)); 
float B = 0.45 (theta2/(theta2+0.09)); 
float acosNV = acos(NV); 
float acosNL = acos(NL); 
float alpha = max(acosNV,acosNL); 
float beta = min(acosNV,acosNL); 
float gamma = length(V - NNV) * length(L - N*NL); 
float Diffuse = 1; 
float OrenNayer = Diffuse * NL (A+ Bmax(0,gamma)*sin(alpha)*tan(beta)); 
FinalColor = OrenNayer;

hh:D

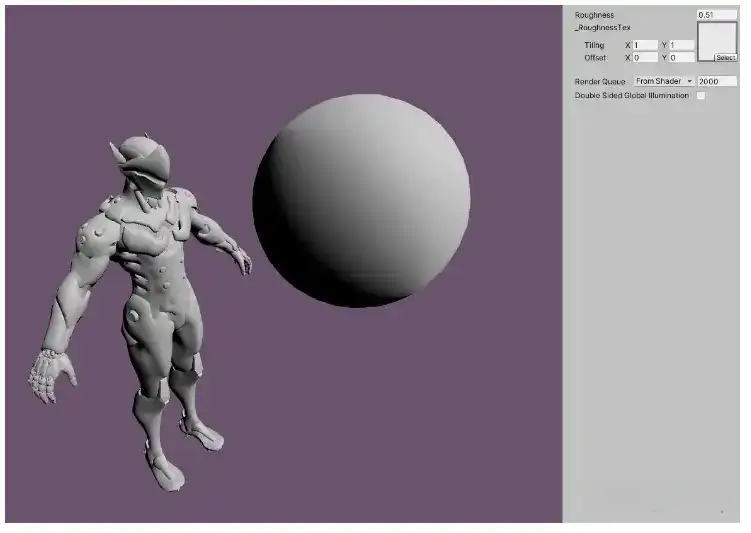
BackLight

先看图片:

概念:

反射:入射光与反射光在表面的同一侧，且入射点与反射点相同

次表面散射:入射光与反射光在表面的同一侧，且入射点与反射点不同

透射:入射光与反射光在表面的不同侧，即光线投过了物体

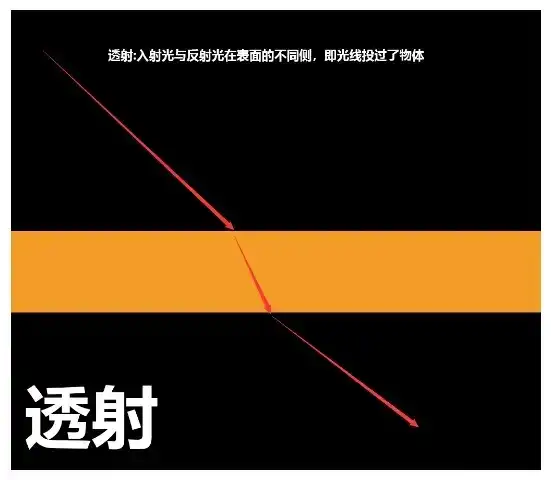
时常有人把透射与次表面散射弄混，因为这两种现象看起来那么像，且真实光照总是包括这三种 "射"的情况。

为了实现这种背面透光的效果，我们可以假定，在主光的反方向还有一个 补光，用这个补光去做一些运算的骚操作即可模拟 背面透光的效果，比如说 沿补光 偏移 反法线 ，等价于，沿主光偏移法线 最后在取反。

//两者是等价的
N_Shift= -N*x + (-L)
N_Shift = -(N*x + L)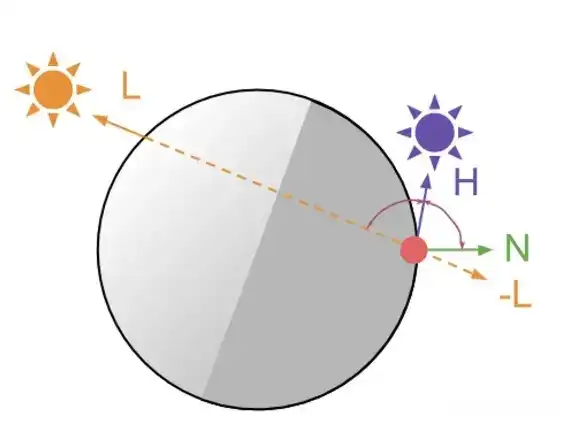

(https://www.alanzucconi.com/2017/08/30/fast-subsurface-scattering-2/)

将N_Shift 当作N去进行光照模型的运算，比如带入Phong模型中。

/模拟透射现象
float _SSSValue =0.6;
float3 N_Shift = -normalize(N*_SSSValue+L);//沿着光线方向上偏移法线，最后在取反
float BackLight = saturate(pow(saturate( dot(N_Shift,V)) ,_PowerValue)*_ScaleValue);
FinalColor = BackLight;

将这个背光效果与前面介绍的Phong 和 Wrap 模型结合一下：

//WrapLight
float WrapLight = pow(dot(N,L)*_WrapValue+(1-_WrapValue),2);
//Blin-Phong
float3 R = reflect(-L,N);
float3 H = normalize(V+L);
// float3 R = normalize(  -L + 2* N* dot(N,L) );
float VR = saturate(dot(V,R));
float NH = saturate(dot(N,H));
float NL = saturate(dot(N,L));
float4 Specular = pow(NH,_SpecularPowerValue)*_SpecularScaleValue;
float4 Diffuse = WrapLight;
 //模拟透射现象
 float _SSSValue =0.6;
 float3 N_Shift = -normalize(N*_SSSValue+L);//沿着光线方向上偏移法线，最后在取反
 float BackLight = saturate(pow(saturate( dot(N_Shift,V)) ,_PowerValue)*_ScaleValue);
 FinalColor =Diffuse + Specular + BackLight;

Anisotropic Lighting

各向异性，Anisotropy，通俗上讲就是在各个方向上所体现出来的性质都不一样。比如在光照下的头发。

可以明显看到一条 "高光带"，而不是 "点状" 高光。为了模拟这种 带状高光，我们在光照方程中使用发丝切线T替代法线N，进行光照计算。为了使高光可以沿着头发移动，需要沿法线的方向偏移切线。为了使高光有点上下偏移使用了一个拉升的噪音贴图。

参考:Hair Rendering and Shading

先计算高光:

//_StretchedNoiseTex 拉升的噪音贴图
float shift = tex2D(_StretchedNoiseTex,i.uv*10).r + _ShiftTangent;
float3 T_Shift = normalize( T+ N*shift);
float3 H = normalize(V+L);
//因为 sin^2+cos^2 =1 所以 sin = sqrt(1-cos^2)
float dotTH = dot(T_Shift,H);
float sinTH = sqrt(1- dotTH*dotTH);

float dirAtten = smoothstep(-1,0,dotTH);
float Specular= dirAtten * pow(sinTH,_AnisotropicPowerValue)*_AnisotropicPowerScale;
FinalColor = Specular;

用真实的物理公式去模拟这种各项异性是非常复杂的，所以都只是视觉上近似模拟。

产生带状的高光是因为使用了sin函数，而sin函数里的变量范围是 [0,1]，所以只会产生一条高光带

可以看一下sin函数的效果：

//设置sin函数的值大于 PI，可以看到多条高光带
FinalColor =sin(length(uv-float2(0.5,0.5)) * 10 *3.1415)

既然sin函数可以，那么cos函数也一定行，因为它们只是相位差了一个 PI/2:

float shift = tex2D(_StretchedNoiseTex,i.uv*4).r + _ShiftTangent;
float3 T_Shift = normalize( T+ N*shift);
float3 H = normalize(V+L);

float dotTH = dot(T_Shift,H);
float cosTH = cos(dot(T_Shift,H));

float dirAtten = smoothstep(-1,0,dotTH);
float Specular = dirAtten * pow(cosTH,_AnisotropicPowerValue)*_AnisotropicPowerScale;

使用cos函数，效果一样，且比使用sin更省性能(因为要开方)

如果想要多条高光带，就像这位飘逸的姐姐

再加几个高光带,可以直接这么写:

//高光带数量
float NumberOfStrip =6;
float cosTh =cos(dot(T_Shift,H)*NumberOfStrip *3.141592654);

在调这个效果的时候，_AnisotropicPowerValue AnisotropicPowerScale 以及 StretchedNoise的uv也要一起调，

Diffuse 用前面的Wraplight

float shift = tex2D(_StretchedNoiseTex,i.uv*4).r + _ShiftTangent;
                
// shift += sin(uv.y*5*3.14);

float3 T_Shift = normalize( T+ N*shift);
float3 H = normalize(V+L);

float dotTH = dot(T_Shift,H);
// float sinTH = sqrt(1- dotTH*dotTH);

// sinTH = sin( acos(dot(T_Shift,H)));
float NumberOfStrip =1;
float cosTH =cos(dot(T_Shift,H)*NumberOfStrip );
// float cosTh =cos(dot(T_Shift,H));
// sinTH = cosTh;

float dirAtten = smoothstep(-1,0,dotTH);
float Specular = dirAtten * pow(cosTH,_AnisotropicPowerValue)*_AnisotropicPowerScale;

float WrapLight = dot(N,L)*0.5+0.5;
float Diffuse = WrapLight;
FinalColor = Diffuse*float4(0.7,0.2,0.4,0) +Specular;

return FinalColor;

高光带有断裂是因为我的_StretchedNoiseTex贴图不连续，整个连续的就行,

调个猛男色，:D

PBR

理论

PBR(Physically Based Shading)是基于与现实世界的物理原理所创建的一种渲染技术，相比于传统的基于经验的模型（Phong Blin-Phong等）更具有物理准确性。基于物理的光照模型必须满足一下三个条件:

1.基于微平面(Microfacet)的表面模型。

2.能量守恒。

3.基于物理的BRDF。

微表面模型

微观尺度上，物体表面有无数的为表面构成。用粗糙度去衡量一个表面的粗糙程度,越粗糙则说明微表面的法线方向越不一致，反射的光越分散，反之则越集中。

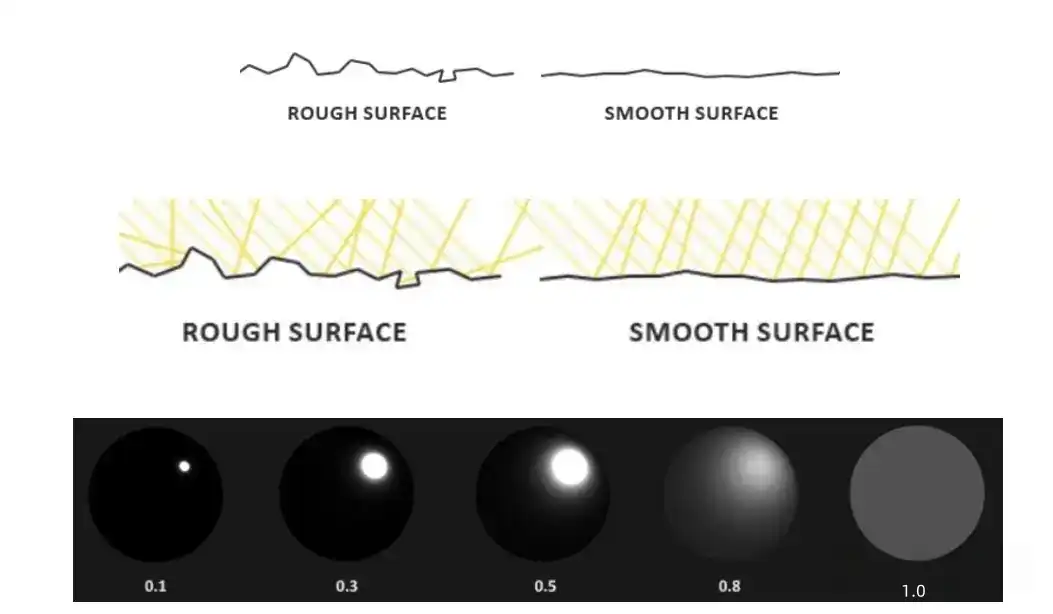
较高的粗糙度值显示出来的镜面反射的轮廓要更大一些。与之相反地，较小的粗糙值显示出的镜面反射轮廓则更小更锐利。

能量守恒

能量守恒定律是自然界普遍的基本定律之一。一般表述为：能量既不会凭空产生，也不会凭空消失，它只会从一种形式转化为另一种形式，或者从一个物体转移到其它物体，而能量的总量保持不变。

将能量守恒定律应用到光照模型中:出射光线的能量永远不能超过入射光线的能量。可以用渲染方程来描述:

在PBR中考虑简化的形式 即反射方程:

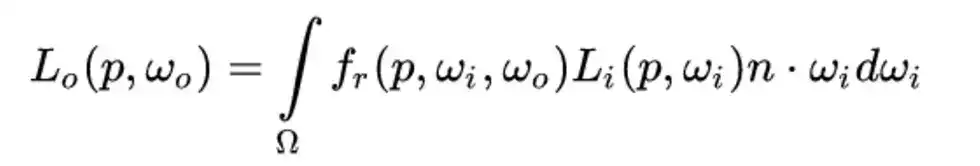
再看这张图:

从上图可以看出随着粗糙度的上升镜面反射区域的面积会增加，作为平衡，镜面反射区域的平均亮度则会下降。

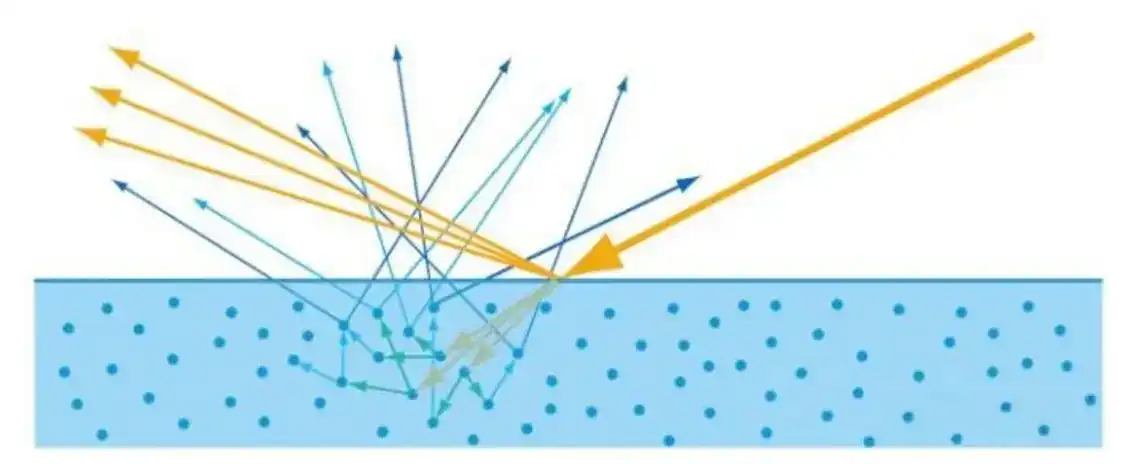
按照能量守恒的关系，首先计算镜面反射部分，它的值等于入射光线被反射的能量所占的百分比。然后漫反射部分就可以直接由镜面反射部分计算得出：

float kS = calculateSpecularComponent(...); // 镜面反射部分
float kD = 1.0 - ks;                        // 漫反射 部分

而在实时渲染中，会有两种光对物体表面造成影响，分别是直接光和间接光，那么与两种反射组合，会有四中光照反射情况。

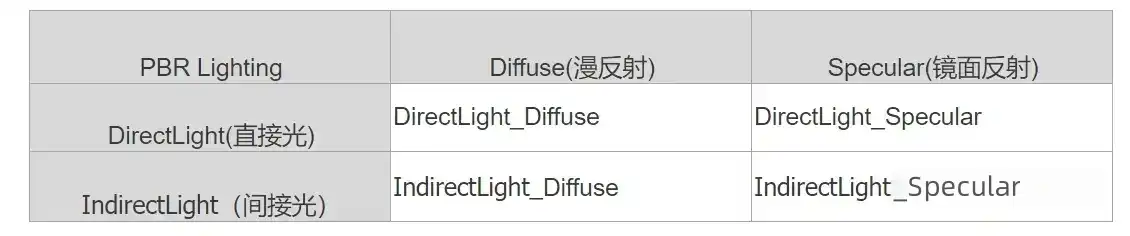
基于物理的BRDF

双向反射分布函数（Bidirectional Reflectance Distribution Function）描述的是入射光和反射光关系。在各种brdf模型中，Cook-Torrance效果更真实应用最广泛。

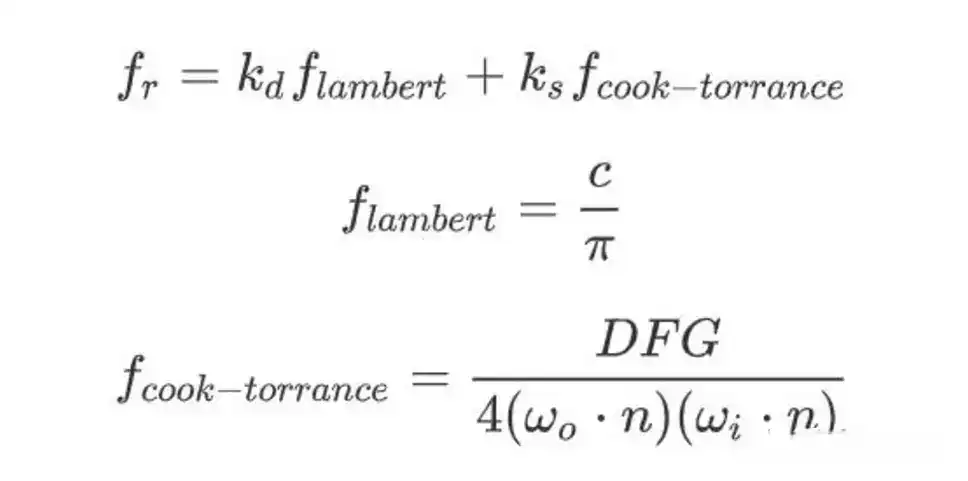
其中Ks是镜面反射所占百分比，Kd是漫反射所占百分比 Kd=1-Ks

将Cook-Torrance带入反射方程中可得:

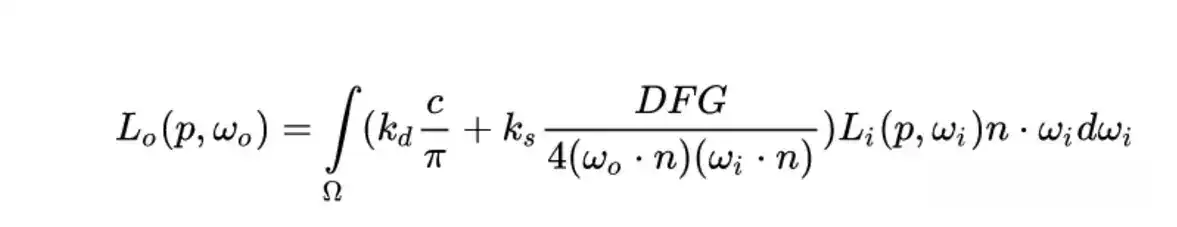
其中F菲涅尔描述了光被反射的比例，代表了反射方程的ks，两者可以合并，所以最终的反射方程为:

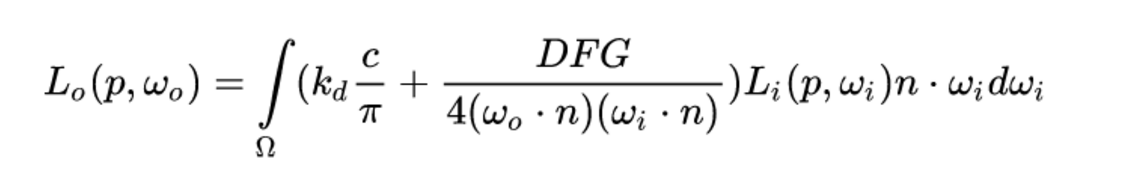
直接光 漫反射+镜面反射
由于直接光通常是 平行光 或者 点光源 都是有限的数量，因此直接将它们的光照结果相加 即是最终的积分结构。我们目前只考虑一个平行光，因此直接光的计算结构 即使积分结果。而间接光从四面八方射到物体表面上来，数量是无限的，因此要用积分计算出所有间接光的计算结果。

直接光的漫反射比较简单:

ks = F;//F的计算参考后面
kd = 1 - ks;
Diffuse = kd*BaseColor/PI;

间接光需要考虑DFG三项

D Distribution of normal function

法线分布函数描述的是微表面的法线方向与半角向量对齐的概率，如果对齐那么认为该反射光可以看到，否则没有。

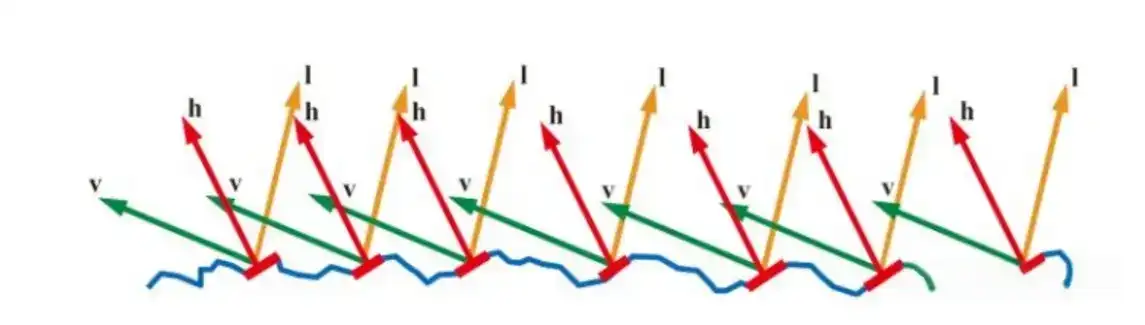
D的Trowbridge-Reitz GGX公式:

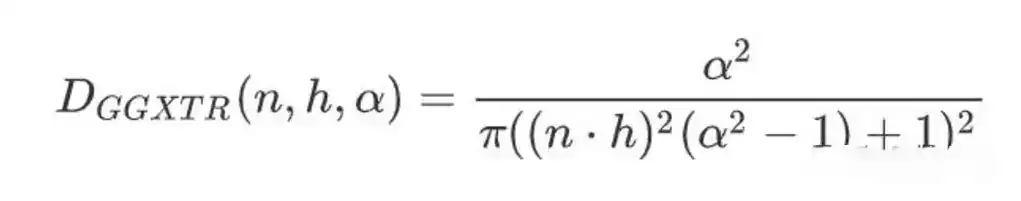
//D
float D_DistributionGGX(float3 N,float3 H,float Roughness)
{
    float a             = Roughness*Roughness;
    float a2            = a*a;
    float NH            = saturate(dot(N,H));
    float NH2           = NH*NH;
    float nominator     = a2;
    float denominator   = (NH2*(a2-1.0)+1.0);
    denominator         = PI * denominator*denominator;
    
    return              nominator/ max(denominator,0.001) ;//防止分母为0
}

仅有D项

float Roughness = 0.356;
FinalColor = D_DistributionGGX(N,H,Roughness);

F Frenel function

如果你站在湖边，低头看脚下的水，你会发现水是透明的，反射不是特别强烈；如果你看远处的湖面，你会发现水并不是透明的，但反射非常强烈。这就是“菲涅尔效应”。简单的讲，就是视线垂直于表面时，反射较弱，而当视线非垂直表面时，夹角越小，反射越明显。如果你看向一个圆球，那圆球中心的反射较弱，靠近边缘较强。

F的Schlick公式:

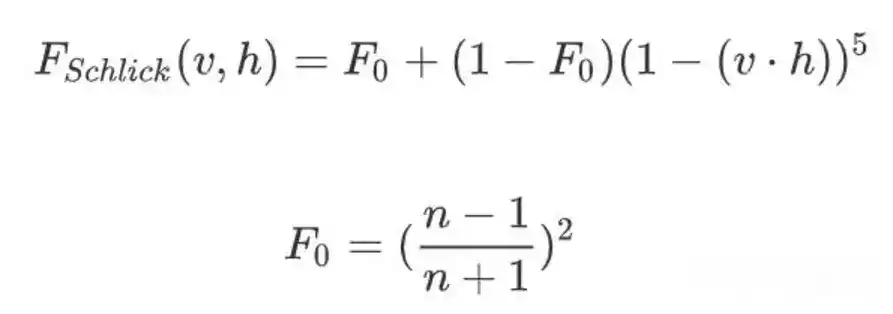
n代表介质的折射率,1为空气的折射率，以下为真实材质测量的F0数值表

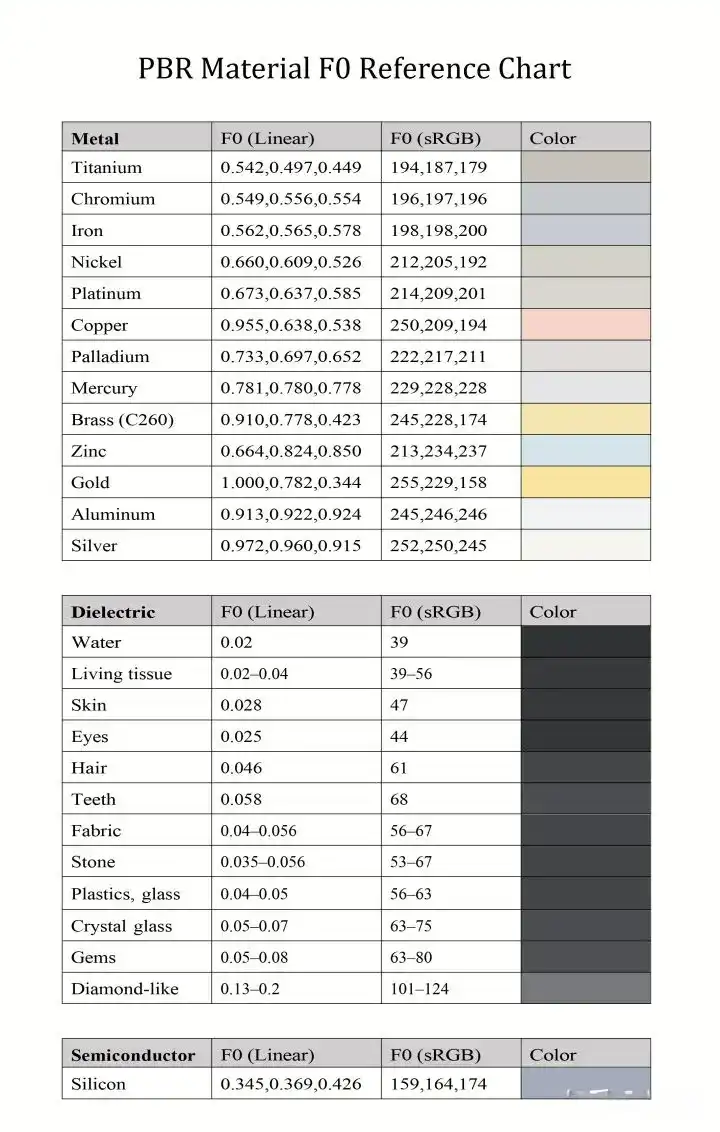
非金属的F0数值较小，金属F0的数值较大，出于简化计算的原因，通过金属度在一个预设的F0和自身颜色之间经行插值。

float3 F0 = 0.04;
F0 = lerp(F0, BaseColor, Metallic);

//F
float3 F_FrenelSchlick(float HV,float3 F0)
{
    return F0 +(1 - F0)*pow(1-HV,5);
    //return lerp(pow(1-HV,5),1,F0);
}

仅有F项:

 float3 BaseColor = float3(1,0.782,0.344);
 float MEtallic = 0.874;
 float3 F0 = 0.04;
 F0 = lerp(F0, BaseColor, Metallic);
 FinalColor = F_FrenelSchlick(HV,F0);

从背面观察:

G Geometry function

几何项体现了微表面的自我遮蔽现象，即入射光线或者反射光线会被自身凹凸不平的表面遮蔽。一般而言，这一项也跟材质的粗糙程度有关，可以理解为越粗超的材质表面越有可能发生自我遮蔽现象。

几何项体现了微表面的自我遮蔽现象，即入射光线或者反射光线会被自身凹凸不平的表面遮蔽。一般而言，这一项也跟材质的粗糙程度有关，可以理解为越粗超的材质表面越有可能发生自我遮蔽现象。

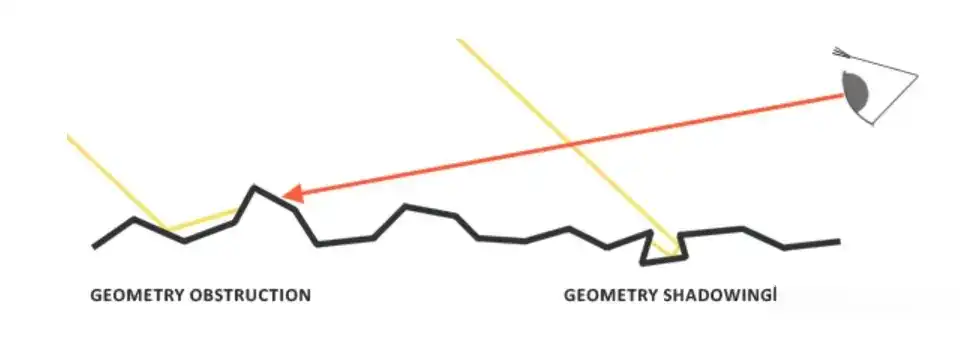
G的Schlick-GGX公式:

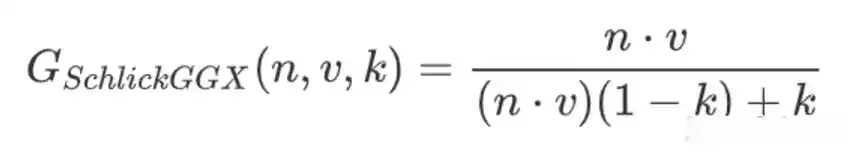
k在直接光与间接光中分别为:

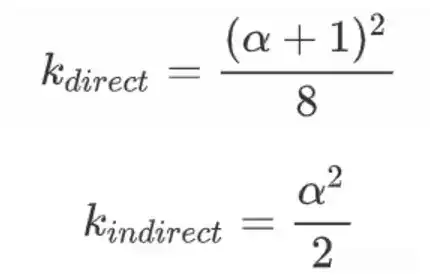
如前面的示意图所示 Smith认为 G项分应该分为为两部分: 第一部分 是 Geometry Obstruction 第二部分是Geometry Shadowing 即:

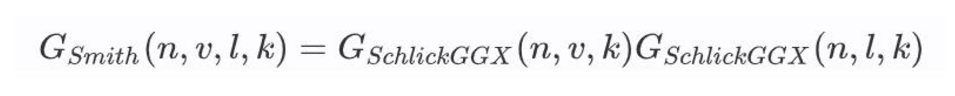
//G
float GeometrySchlickGGX(float NV,float Roughness)
{
    float r = Roughness +1.0;
    float k = r*r / 8.0;      //直接光
    float nominator = NV;
    float denominator = k + (1.0-k) * NV;
    return nominator/ max(denominator,0.001) ;//防止分母为0
}

float G_GeometrySmith(float3 N,float3 V,float3 L,float Roughness)
{
    float NV = saturate(dot(N,V));
    float NL = saturate(dot(N,L));

    float ggx1 = GeometrySchlickGGX(NV,Roughness);
    float ggx2 = GeometrySchlickGGX(NL,Roughness);

    return ggx1*ggx2;

}

仅有G项:

float Roughness = 0.356;
FinalColor = G_GeometrySmith(N,V,L,Roughness);

直接光的最后效果:

//================== PBR ========================= // 
// float3 BaseColor = float3(0.5,0.3,0.2); 
float3 BaseColor = _BaseColor;
float Roughness = _Roughness; 
float Metallic = _Metallic; 
float3 F0 = lerp(0.04,BaseColor,Metallic); 
float3 Radiance = _LightColor0.xyz;

//================== Direct Light ========================= // 
//Specular
//Cook-Torrance BRDF
float HV = saturate(dot(H,V));
float NV = saturate(dot(N,V));
float NL = saturate(dot(N,L));

float D = D_DistributionGGX(N,H,Roughness);
float3 F = F_FrenelSchlick(HV,F0);
float G = G_GeometrySmith(N,V,L,Roughness);

float3 KS = F;
float3 KD = 1-KS;
KD*=1-Metallic;
float3 nominator = D*F*G;
float denominator = max(4*NV*NL,0.001);
float3 Specular = nominator/denominator;

//Diffuse
float3 Diffuse = KD * BaseColor / PI;
float3 DirectLight = (Diffuse + Specular)*NL *Radiance;
FinalColor.rgb = DirectLight.rgb;

间接光 漫反射+镜面反射

间接光是用IBL(Image Based Lighting)来模拟的。与直接光相比，IBL把周围环境整体视为一个大光源，IBL 通常使用（取自现实世界或从3D场景生成的）环境立方体贴图 (Cubemap) ，我们可以将立方体贴图的每个像素视为光源，在渲染方程中直接使用它。这种方式可以有效地捕捉环境的全局光照和氛围，使物体更好地融入其环境。

表示环境或场景辐照度的一种方式是（预处理过的）环境立方体贴图，给定这样的立方体贴图，可以将立方体贴图的每个纹素视为一个光源。使用一个方向向量 wi 对此立方体贴图进行采样，就可以获取该方向上的场景辐照度。

给定方向向量 wi ，获取此方向上场景辐射度的方法就简化为：

float3 radiance = tex2D(_CubemapEnvironment, lightDirection).rgb;  

虽然这么简化了，但是如果要求解反射方程的话，我们依然需要计算球面积分，这对于实时渲染来说太昂贵了。解决这个问题，我们可以通过预计算一些结果并存储起来，然后在运行时利用这些中间结果计算最终值。首先将反射方程拆分一下。

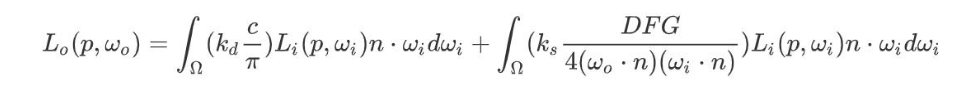
通过将积分分成两部分，可以分开研究漫反射和镜面反射部分。

间接光漫反射部分：

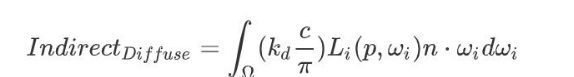
间接光镜面反射部分：

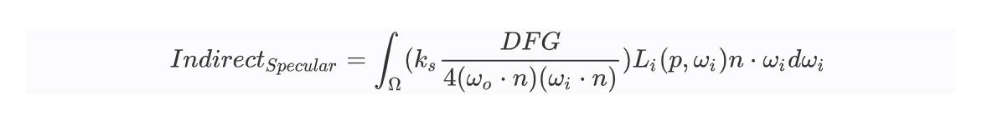
漫反射部分

颜色 c 、折射率 kd 和 π 在整个积分是常数，不依赖于任何积分变量。基于此，可以将常数项移出漫反射积分：

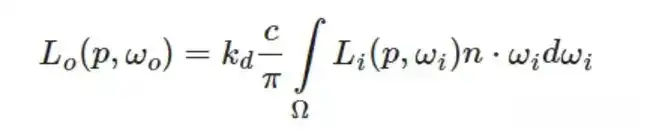
这给了我们一个只依赖于 wi 的积分（假设 p 位于环境贴图的中心）。有了这些知识，我们就可以计算或预计算一个新的立方体贴图，它在每个采样方向——也就是纹素——中存储漫反射积分的结果，这些结果是通过卷积计算出来的。

卷积的特性是，对数据集中的一个条目做一些计算时，要考虑到数据集中的所有其他条目。这里的数据集就是场景的辐射度或环境贴图。因此，要对立方体贴图中的每个采样方向做计算，我们都会考虑半球 Ω 上的所有其他采样方向。

为了对环境贴图进行卷积，我们通过对半球 Ω 上的大量方向进行离散采样并对其辐射度取平均值，来计算每个输出采样方向 wo 的积分。以wo方向所在的半球，采样方向 wi 。

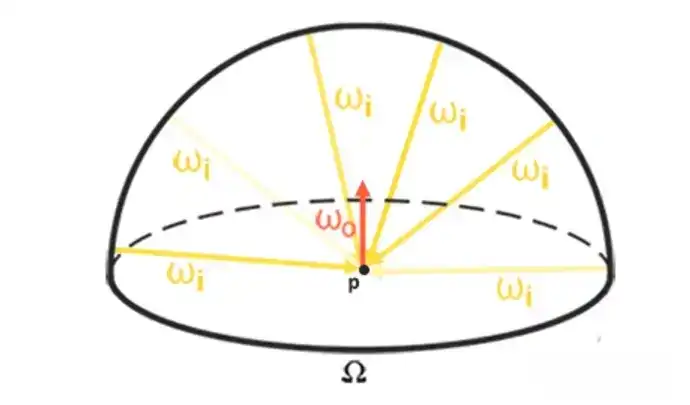
这个预计算的立方体贴图，在每个采样方向 wo 上存储其积分结果，可以理解为场景中所有能够击中面向 wo 的表面的间接漫反射光的预计算总和。这样的立方体贴图被称为辐照度贴图，因为经过卷积计算的立方体贴图能让我们从任何方向有效地直接采样场景（预计算好的）辐照度。

对于一点P 它所受间接光来自整个CubeMap (以CubeMap中的每个像素为一个光源) ，假设P点的法线N为光线的出射方向，那么可以离线计算出P点所受环境光照的影响。给定任何方向向量 wi ，我们可以对预计算的辐照度图采样以获取方向 wi 的总漫反射辐照度。为了确定片段上间接漫反射光的数量（辐照度），我们获取以表面法线为中心的半球的总辐照度。获取场景辐照度的方法就简化为：

float3 irradiance = tex3D(irradianceMap, N);

生成辐照度贴图

实时进行积分计算太消耗，可以先离线计算出来。然而，理论上在半球上采样方向是无限的 ,因此不可能从 半球上 的所有方向采样环境光照。不过我们可以对有限数量的方向采样以近似求解，在半球内均匀间隔或随机取方向可以获得一个近似精确的辐照度值，从而离散地计算积分结果。

伪代码:

//Normal为当前点P的 采样方向
以Normal方向为半球，获取一组随机的方向 且将其定义为Normals 
float3 avg =0
foreach( N in Normals)
{
    avg = SampleCube(CubeMap,N)
}
avg /= Normals.Count
//avg 则是 所有环境光 对当前点P的最终影响结果
IrradianceMap.SetValue(avg,Normal) //将结果储存在辐照度贴图中 

LightProbe 与 球协函数

辐照度贴图是固定的，如果游戏中有多个场景，比如室内室外 那么肯定是不能为每一个场景都单独弄一个辐照度贴图的，会消耗大量内存。游戏引擎中使用LightProbe放置在场景中，去近似采样并存储以该LightProbe为中心的 "辐照度贴图"，但不是单独存一张贴图，而是用球协函数存储相应的信息，最终存储的是球协函数的参数，通常是 9个float，这比单独存一张贴图节省多了。

在Unity 中放置LightProbe，并且烘培后，使用ShadeSH9函数即可获取当前的点的"辐照度"。

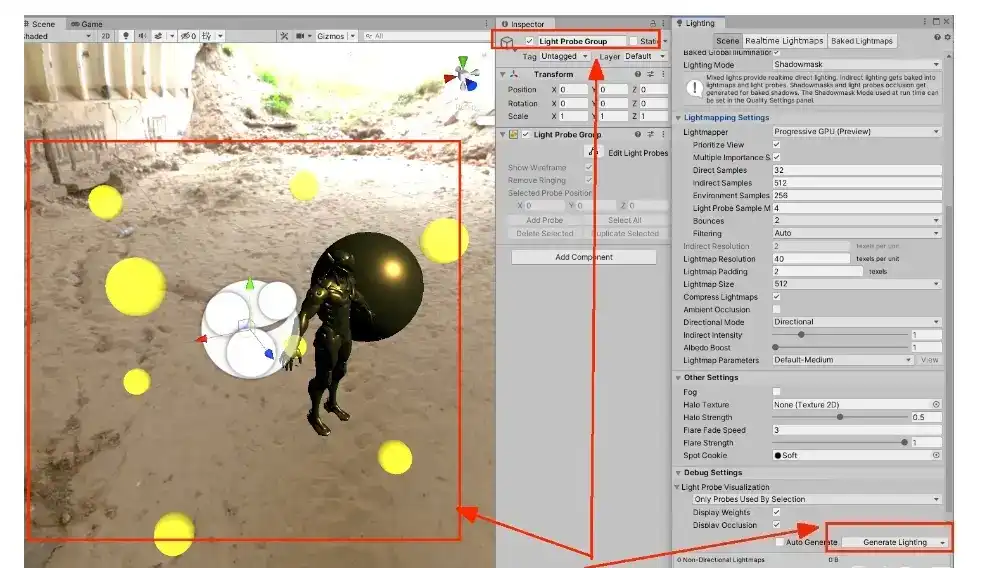
仅显示球协函数的光照:

//注意需要设置 Tags{ "LightMode"="ForwardBase"} 才能正确得到球鞋函数值
//否则ShadeSh9返回值为0 
float3 irradianceSH = ShadeSH9(float4(N,1)));
FinalColor.rgb = irradianceSH;

HDR图可以在这里下载: hdrihaven.com/hdris/

仅显示间接光漫反射:

float3 irradianceSH = ShadeSH9(float4(N,1));
return irradianceSH.rgbb;
float3 Diffuse_Indirect = irradianceSH * BaseColor / PI *KD_IndirectLight;
FinalColor.rgb = Diffuse_Indirect;

骚操作一下:

将上面的HDR图直接在PS里做一个高斯模糊，然后再去采样

float3 EnvCubeMap = texCUBE(_EnvCubeMap,N).xyz;
return (EnvCubeMap.xyzz);

得到下面结果:

会比较暗，这是因为在PS做模糊的时候，将HDR从32位转为了16位，因此手动把精度加回来(不准确，但是可以理解这个过程)

float3 EnvCubeMap = texCUBE(_EnvCubeMap,N).xyz;
//用ToneMaping HDR=>LDR
//x3.75 是为了补救损失的精度
return ACESToneMapping(EnvCubeMap.xyzz*3.75);

和球协的有点区别，但是明显这张图比球协的更准确地反映了 环境光 的 "黄"

球协函数原理参考：

https://pdfs.semanticscholar.org/83d9/28031e78f15d9813061b53d25a4e0274c751.pdf

https://basesandframes.files.wordpress.com/2016/05/spherical-harmonic-lighting-gdc-2003.pdf

http://web.cs.wpi.edu/~emmanuel/courses/cs563/S05/talks/mark_w5_spherical_harmonic_lighting.pdf

镜面反射部分

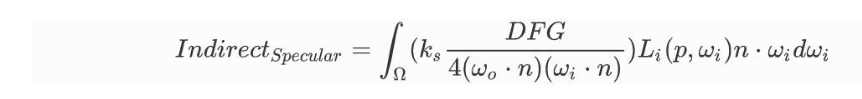
将镜面反射的公式近似地拆成两部分（EpicGames SplitSum）

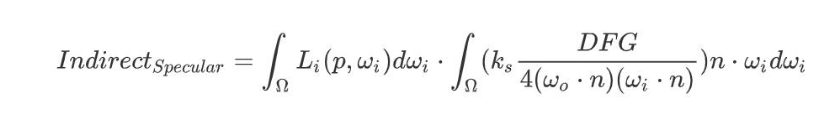
间接光镜面积分第一部分

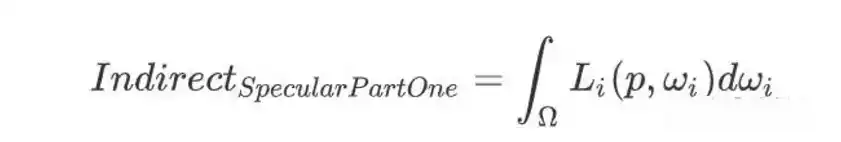
对于高光部分而言，如果材质表面越光滑，则该点出射光大部分贡献来源于入射光的镜面反射，很小一部分来源于各个方向的漫反射。所以，这次我们在计算积分的时候，需要把粗糙度也考虑进去。如果粗糙度越低，那么积分的贡献范围就越集中，相当于卷积核的面积越小，大权重集中在核中心，卷积结果尺寸越大，产生越清晰的反射效果。反之亦然。

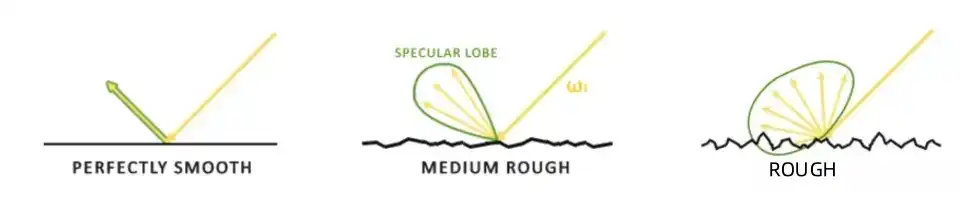
于是可以根据材质的粗糙度，映射到某个粗糙度区间，然后把计算结果保存到不同的LOD等级中。这张具有不同LOD等级的立方体贴图也称为pre-filtered environment map。

后续在运行时只需要根据粗糙等级做一次采样就可以得到高光积分的第一部分。

//UNITY_SPECCUBE_LOD_STEPS 在  "UnityStandardConfig.cginc"中 
// #define UNITY_SPECCUBE_LOD_STEPS 6
float mip = Roughness*(1.7 - 0.7*Roughness) * UNITY_SPECCUBE_LOD_STEPS ; 
float4 rgb_mip = UNITY_SAMPLE_TEXCUBE_LOD(unity_SpecCube0,R,mip);
//间接光镜面反射采样的预过滤环境贴图
//unity_SpecCube0_HDR储存的是 最近的ReflectionProbe
float3 EnvSpecularPrefilted = DecodeHDR(rgb_mip, unity_SpecCube0_HDR);
FinalColor.rgb = EnvSpecularPrefilted.rgb;

仅显示ReflectionProbe信息，即 间接光镜面积分第一部分 结果

ReflectionProbe

Reflection Probe 是六个相机分别捕捉它所在位置的6个方向的场景信息，最后储存在一张Cubemap贴图里。

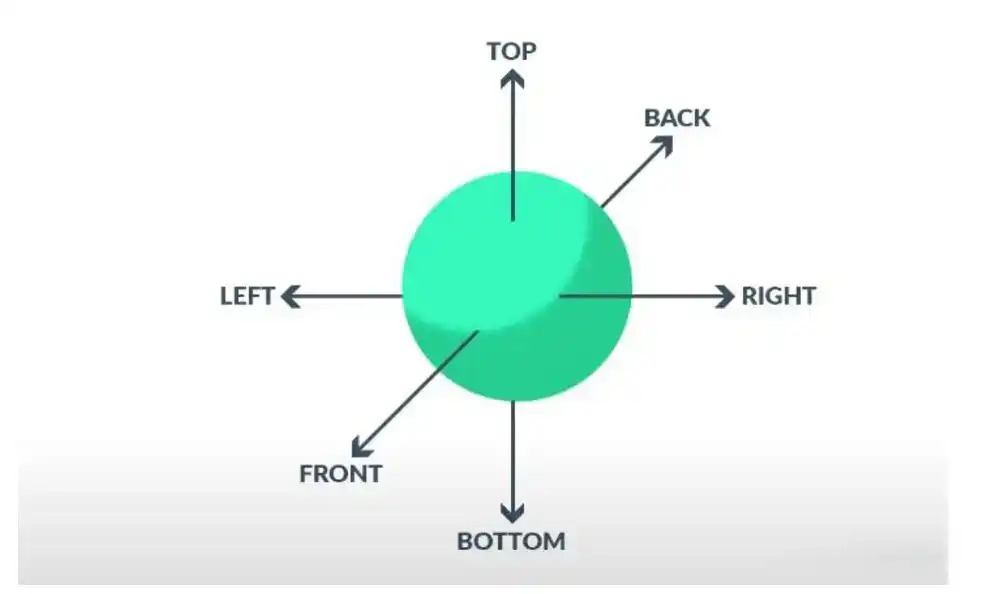
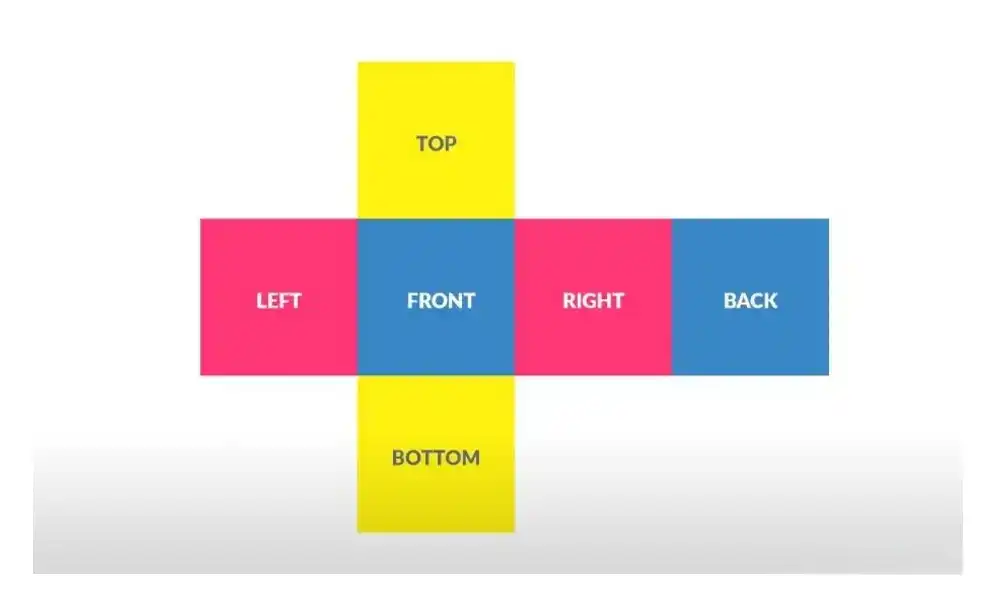
在场景中放置ReflectionProbe Bake之后才会有信息。

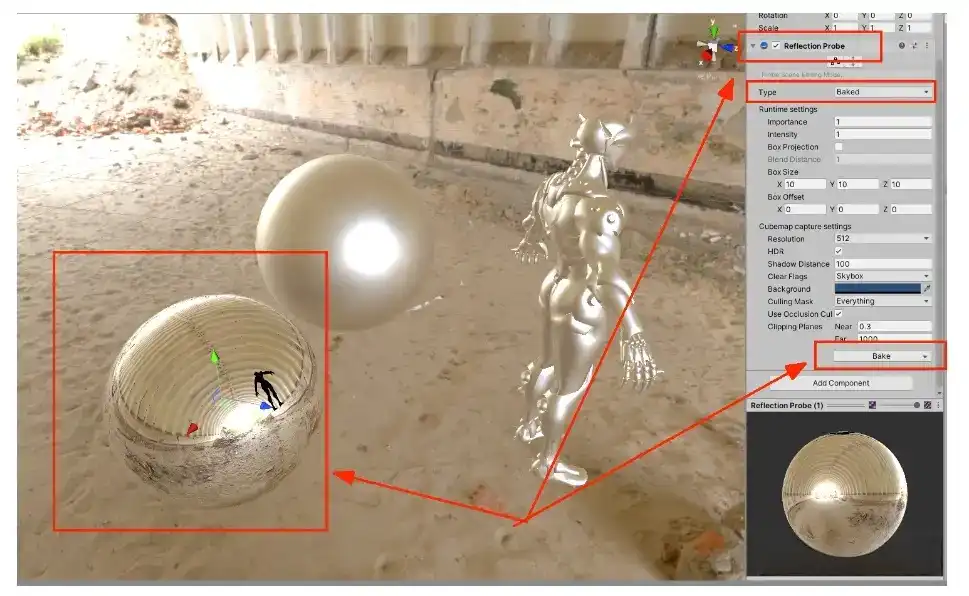
当用一个未烘培过的ReflectionProbe去靠近物体(仅显示ReflectionProbe信息)，明显发现物体变黑了，因为这个未烘培过的ReflectionProbe没有信息，而unity_SpecCube0是最近的一个ReflectionProbe。

间接光镜面积分第二部分

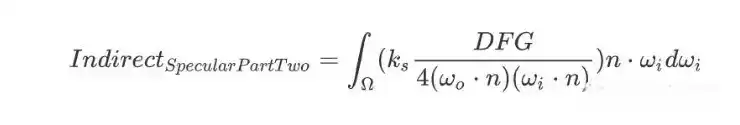
经过推导后可得如下：

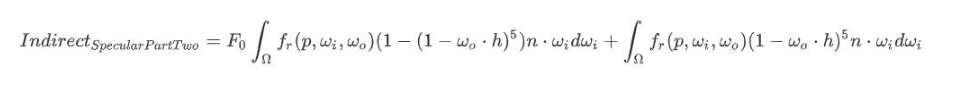
计算这个积分有两种办法，第一种是BRDF积分图 第二种是 函数拟合

BrdfLut

假设每个方向的入射光都是白色的（L(p,x)=1.0 ），就可以在给定粗糙度、光线 ωi 法线 n 夹角 n⋅ωi 的情况下，预计算 BRDF 的响应结果。以X轴为法线与入射光的夹角(dot(N,L))，以Y轴为粗糙度，将计算的结果存储在一张 2D 贴图上(Lut)，该贴图称为BRDF积分贴图。积分的结果分别储存在 贴图的 RG通道中。使用的时候可以直接采样该贴图即可。

float3 F_IndirectLight = FresnelSchlickRoughness(NV,F0,Roughness);
float2 env_brdf = tex2D(_BRDFLUTTex, float2(NV, Roughness)).rg;
float3 IndirectLightSpecularPartTwo = F_IndirectLight * env_brdf.r + env_brdf.g;
FinalColor.rgb = IndirectLightSpecularPartTwo ;

仅显示Specular PartTwo

上面代码中的菲涅尔系数计算和前面的有两点不同，第一点是这里没有用于计算微片元朝向的D函数，计算菲涅尔系数使用的是真正的nv而不是vh，第二点是考虑了粗糙度。使用nv是由于环境光来自半球内围绕法线N的所有方向，因此无法和直接光照中的法线分布函数D一样使用单个半角向量来确定微平面分布，所以在此我们只能使用法线和视线的夹角（即nv）来计算菲涅尔效果。

float3 FresnelSchlickRoughness(float NV,float3 F0,float Roughness)
{
    return F0 + (max(float3(1.0 - Roughness, 1.0 - Roughness, 1.0 - Roughness), F0) - F0) * pow(1.0 - NV, 5.0);
}

数值拟合

PartTwo的结果出了可以预计算出来外，还可以用函数拟合来实时计算。

// 这是使命召唤黑色行动2的函数拟合 Black Ops II
float2 EnvBRDFApprox_BlackOp2(float Roughness, float NV)
{
    float g = 1 -Roughness;
    float4 t = float4(1/0.96, 0.475, (0.0275 - 0.25*0.04)/0.96, 0.25);
    t *= float4(g, g, g, g);
    t += float4(0, 0, (0.015 - 0.75*0.04)/0.96, 0.75);
    float A = t.x * min(t.y, exp2(-9.28 * NV)) + t.z;
    float B = t.w;
    return float2 ( t.w-A,A);
}

//UE4 在 黑色行动2 上的修改版本
float2 EnvBRDFApprox_UE4(float Roughness, float NoV )
{
    // [ Lazarov 2013, "Getting More Physical in Call of Duty: Black Ops II" ]
    // Adaptation to fit our G term.
    const float4 c0 = { -1, -0.0275, -0.572, 0.022 };
    const float4 c1 = { 1, 0.0425, 1.04, -0.04 };
    float4 r = Roughness * c0 + c1;
    float a004 = min( r.x * r.x, exp2( -9.28 * NoV ) ) * r.x + r.y;
    float2 AB = float2( -1.04, 1.04 ) * a004 + r.zw;
    return AB;
}

float3 F_IndirectLight = FresnelSchlickRoughness(NV,F0,Roughness);
float2 env_brdf = EnvBRDFApprox_UE4(Roughness,NV);
float3 IndirectLightSpecularPartTwo = F_IndirectLight * env_brdf.r + env_brdf.g;
FinalColor.rgb = IndirectLightSpecularPartTwo ;

用函数拟合的效果比BrdfLut的 效果更好，且更节省性能。

关于BrdfLut的生产参考:

https://learnopengl.com/PBR/IBL/Specular-IBL

数值拟合的参考:

https://blog.selfshadow.com/publications/s2013-shading-course/lazarov/s2013_pbs_black_ops_2_slides_v2.pptx

公式推导参考：

https://blog.selfshadow.com/publications/s2013-shading-course/karis/s2013_pbs_epic_notes_v2.pdf

最终效果:

//================== Direct Light ============================================== //
//Specular
//Cook-Torrance BRDF
float HV = saturate(dot(H,V)); 
float NV = saturate(dot(N,V)); 
float NL = saturate(dot(N,L));

float D = D_DistributionGGX(N,H,Roughness);
float3 F = F_FrenelSchlick(HV,F0); 
float G = G_GeometrySmith(N,V,L,Roughness);

float3 KS = F; 
float3 KD = 1-KS; 
KD*=1-Metallic; 
float3 nominator = DFG; 
float denominator = max(4NVNL,0.001); 
float3 Specular = nominator/denominator; 
//Diffuse 
float3 Diffuse = KD * BaseColor / PI;

float3 DirectLight = (Diffuse + Specular)*NL *Radiance;
//================== Indirect Light ============================================== //
float3 IndirectLight = 0; 
//Specular 
float3 R = reflect(-V,N); 
float3 F_IndirectLight = FresnelSchlickRoughness(NV,F0,Roughness); 
// float3 F_IndirectLight = F_FrenelSchlick(NV,F0); 
float mip = Roughness*(1.7 - 0.7*Roughness) * UNITY_SPECCUBE_LOD_STEPS ; 
float4 rgb_mip = UNITY_SAMPLE_TEXCUBE_LOD(unity_SpecCube0,R,mip);

//间接光镜面反射采样的预过滤环境贴图
float3 EnvSpecularPrefilted = DecodeHDR(rgb_mip, unity_SpecCube0_HDR);

//LUT采样
// float2 env_brdf = tex2D(_BRDFLUTTex, float2(NV, Roughness)).rg; //0.356

//数值近似
float2 env_brdf = EnvBRDFApprox(Roughness,NV);
float3 Specular_Indirect = EnvSpecularPrefilted * (F_IndirectLight * env_brdf.r + env_brdf.g);

//Diffuse
float3 KD_IndirectLight = 1 - F_IndirectLight;
KD_IndirectLight *= 1 - Metallic;
float3 irradianceSH = ShadeSH9(float4(N,1));
float3 Diffuse_Indirect = irradianceSH * BaseColor / PI *KD_IndirectLight;
IndirectLight = Diffuse_Indirect + Specular_Indirect;

float4 FinalColor =0;
FinalColor.rgb = DirectLight + IndirectLight;

与Unity默认的对比 BaseColor=(255,199,88) Metallic=0.95 Roughness=0.21 参数一致 用屏幕后处理统一做 ToneMapping

可以看出Unity 的效果偏亮一点，因为Unity在实现PBR算法的时候 直接光漫反射 与 间接光漫反射 都没有除以PI(为了与老版本效果兼容)，而我们的算法是标准的PBR算法，在表现金属上会有更细腻的亚光效果。

完整的PBR效果:(BaseColor + Metallic +Roughness + Normal + AO)

完整的PBR代码链接:

Unity-Basic-Shader/PBR_BetterThanUnity.shader at master · ipud2/Unity-Basic-Shader · GitHub

HDR 与 Gamma

HDR

在PBR中做光照运算时，最终输出的颜色值时常超过1，而超过1的部分在显示器中显示就会 “泛白过爆”，为了解决这个问题，将HDR(High Dynamic Range)的颜色值转换到LDR(Low Dynamic Range)

的算法叫做 ToneMapping(色调映射)。在各种ToneMapping算法中ACESTonemapping效果与性能兼优。

 float3 ACESToneMapping(float3 x)
{
    float a = 2.51f;
    float b = 0.03f;
    float c = 2.43f;
    float d = 0.59f;
    float e = 0.14f;
    return saturate((x*(a*x+b))/(x*(c*x+d)+e));
}

Gamma

1. 人眼对 低亮度 的颜色变化 感知强，对 高亮度 的颜色变化 感知弱

2. 为了提高图片的显示辨识度，将自然界线性的颜色储存在非线性的空间(Gamma)

3. 在渲染中先将图片转化为 线性空间(Linear)，再进行颜色加减乘除操作才是正确的，最后再转为非线性(Gamma)的颜色输出

//Gamma => Linear
float3 Color_Linear = pow(Color_Gamma,2.2);
//Linear => Gamma
float3 Color_Gamma= pow(Color_Linear,1/2.2);

在Unity中如果设置颜色空间为Gamma，那么在进行PBR计算之前需要用代码手动转到Linear,并且最终输出到显示器的颜色时候 需用代码手动转到Gamma空间

在Unity中如果设置颜色空间为Linear，那么Unity会帮我们把图片自动转到Linear空间，并且最终输出到显示器的颜色时候 自动转到Gamma空间

总结

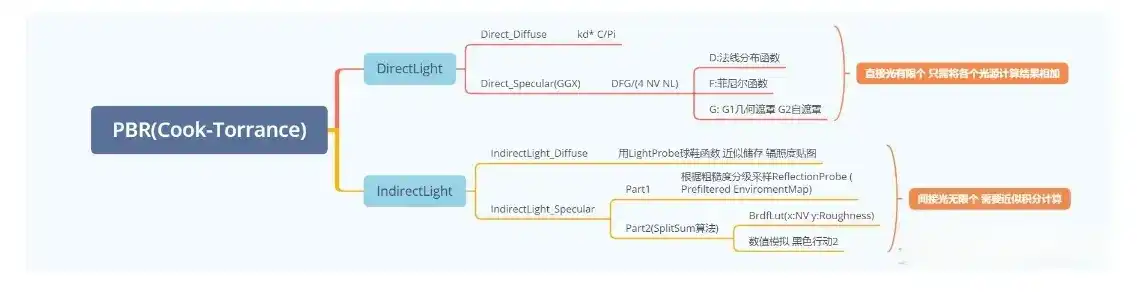
PBR Anistropy 基于物理的各项异性高光

todo

结果

代码:Unity-Basic-Shader/基于物理的高光Brdf/PBRAnistropicSpecular.shader at master · ipud2/Unity-Basic-Shader · GitHub

ClearCoat清漆

传统的PBR可以很好地模拟出各项同性的单层表面的光照模型，但是对于多层材质就很难模拟出。比如常见的清漆效果(ClearCoat)。

以下图片是一个对比:

为了模拟这种清漆效果，可以再原PBR的基础上加一个二级高光，但要保证能量守恒，那么能量守恒公式可以这么描述:

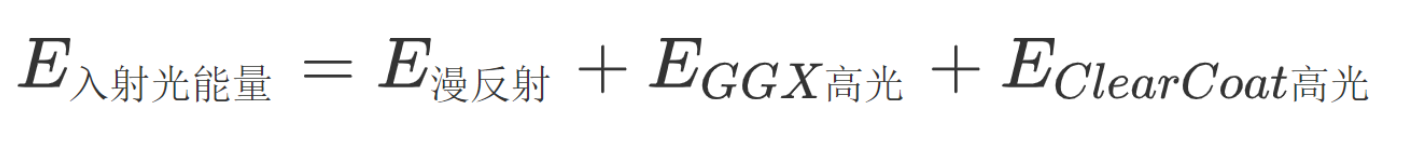
对于清漆材质，物体的表面分为两部分，上面的一部分是ClearCoatLayer 下面的部分是BaseLayer，一束光入射到表面，一部分光直接反射出去(ClearCoat高光，且忽略这部分光的漫反射),另一部分进入BaseLayer，再分为漫反射与GGX高光反射出去。

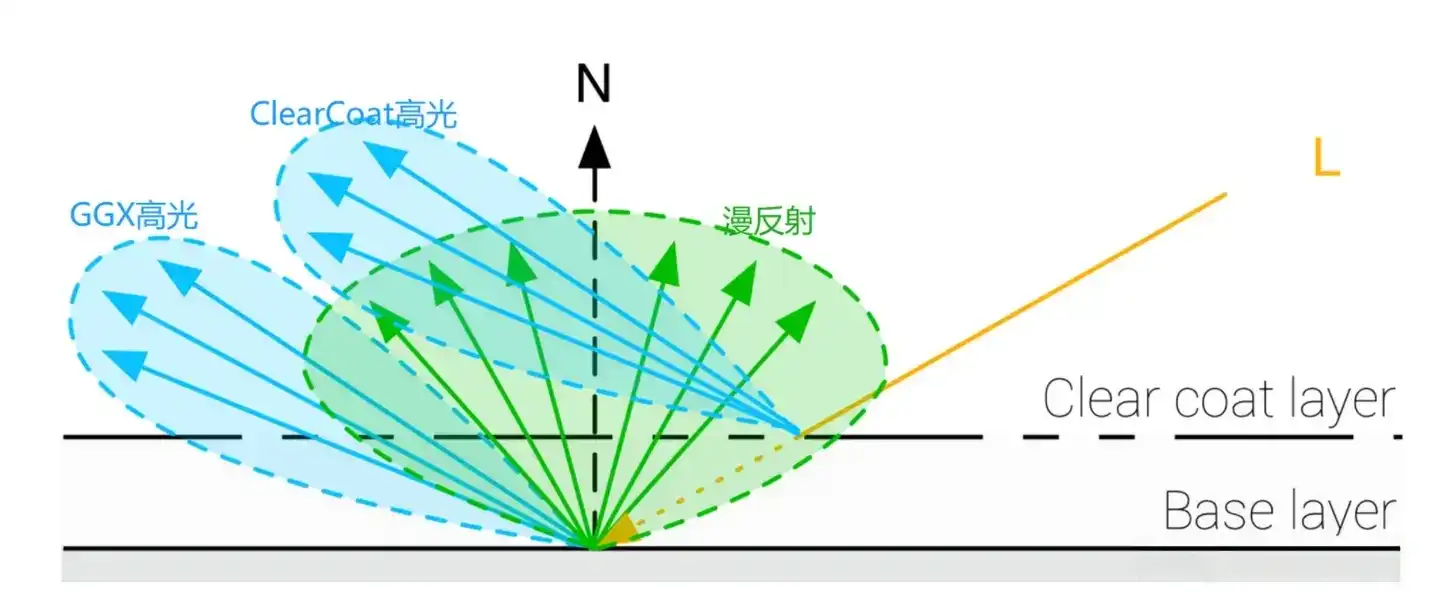
那么现在要解决的问题就是:有多少光进入了BaseLayer？ 为了解决这个问题，引入了两个参数，ClearCoatRoughness用来描述清漆表面的粗糙度以及ClearCoatIntensity用来描述清漆反射的强度。清漆表面的菲尼尔反射部分属于ClearCoatLayer的能量，剩下的进入BaseLayer。用公式描述:

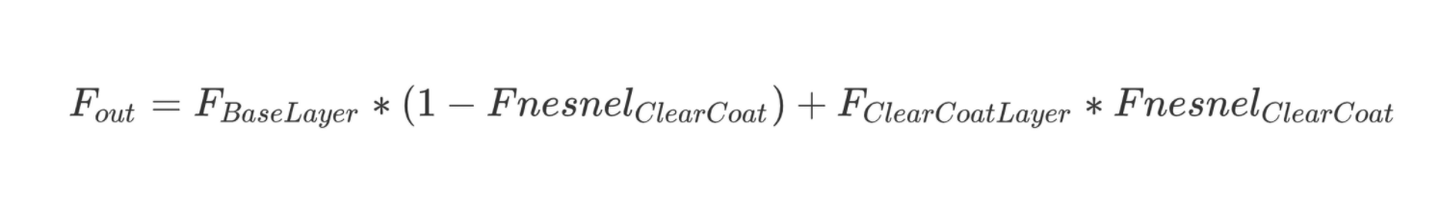
ClearCoat高光用GGX来描述，因为GGX中有Fresnel部分就不用额外在额外乘以菲尼尔项了。公式可以简化为:

对于直接光部分的代码

//Diffuse为直接光漫反射,Specular为直接光高光
float3 DirectLight = (Diffuse + Specular)*NL *Radiance;
float F_ClearCoat = F_FrenelSchlick(HV,0.04)*_ClearCoat;
float3 Specular_ClearCoat = Specular_GGX(N,L,H,V,NV,NL,HV,_RoughnessClearCoat,0.04)*_ClearCoat;
//保证能量守恒
DirectLight = DirectLight * (1-F_ClearCoat) + Specular_ClearCoat;

对于间接光部分的代码

//Diffuse_Indirect为间接光漫反射,Specular_Indirect为间接光高光
IndirectLight = (Diffuse_Indirect + Specular_Indirect);
float3 Specular_Indirect_ClearCoat = SpecularIndirect(N,V,_RoughnessClearCoat,0.04)*_ClearCoat;
float3 F_IndirectLight_ClearCoat = FresnelSchlickRoughness(NV,0.04,_RoughnessClearCoat)*_ClearCoat;
//保证能量守恒
IndirectLight = IndirectLight*(1-F_IndirectLight_ClearCoat) +Specular_Indirect_ClearCoat;

最后结果:

完整代码连接:Unity-Basic-Shader/光照模型/ClearCoat.shader at master · ipud2/Unity-Basic-Shader · GitHub

Cloth布料

TODO原理:

结果:

完整代码连接:Unity-Basic-Shader/光照模型/Cloth.shader at master · ipud2/Unity-Basic-Shader · GitHub

总结

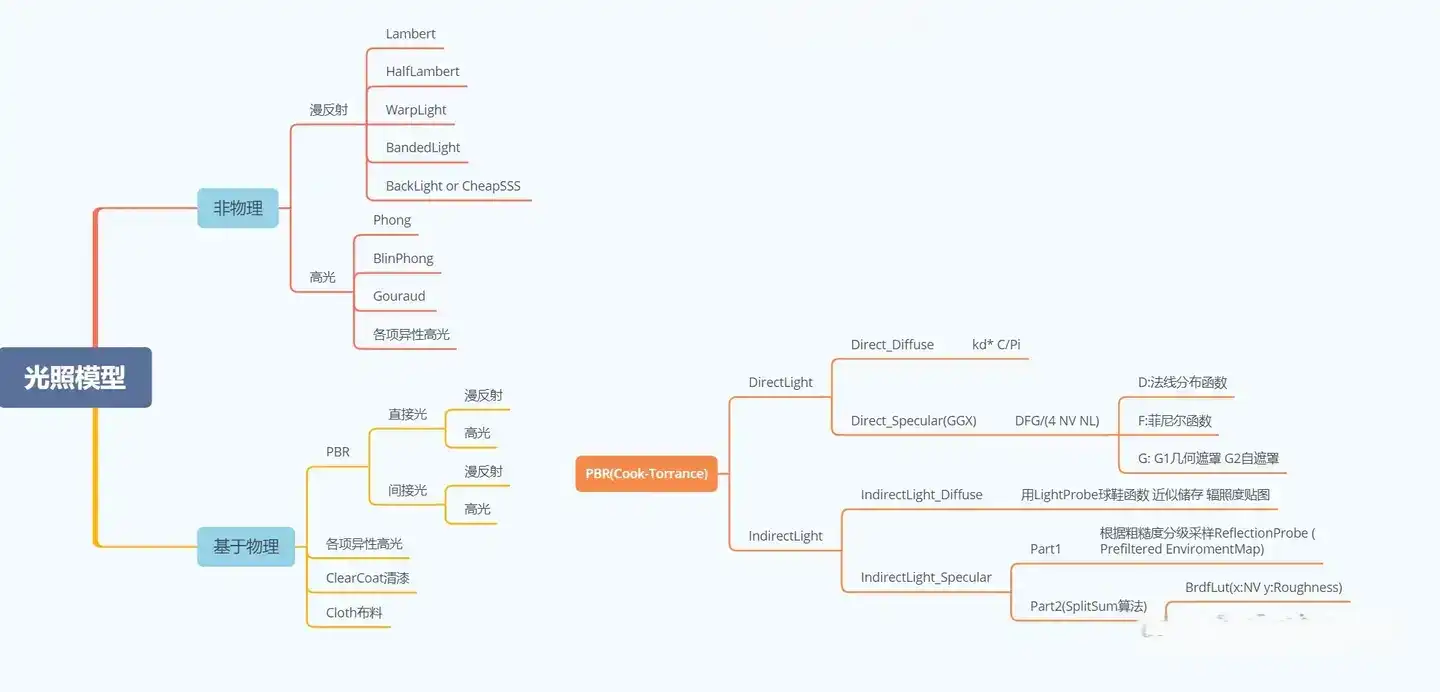
TODO: NPR Skin Hair Eye